Introduction

In a blog post titled “Build a Two-Digit ‘Adder Bug’ with Evolutionary Algorithms,” the author introduces a captivating project on constructing a two-digit “adder bug.” This “adder bug” has four input points, three output points, and 27 gates, each with two input points and one output point. These points are interconnected, and every time the bug reproduces, the connections change randomly. The bugs are tested with two-digit addition problems, and those that solve more problems correctly have a higher chance of reproducing and surviving when the bug population reaches its limit.

This intriguing project piqued my interest, and I have always wanted to run it myself. Unfortunately, the source code for this project is missing, as noted by the original author.

After days of development, I managed to redevelop the project, which is now available on GitHub. In this blog, I will introduce the details of my recreation process and the challenges I faced during development.

Background of the Adder

To provide a comprehensive understanding of the project, let’s delve into the design of an adder. We will explore what a logic gate is and how these gates are used to compose an adder.

Logic Gate

According to Wikipedia, “A logic gate is a device that performs a Boolean function, a logical operation performed on one or more binary inputs that produces a single binary output.”

There are four basic types of gates: AND, OR, XOR, and NOT.

The input and output functions are illustrated below.

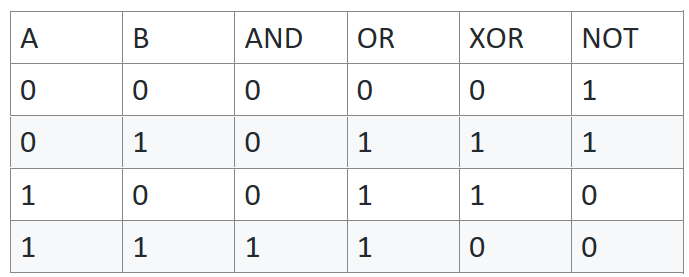
Note that the NOT gate only requires one input, so it uses the first input and disregards the second. Typically, the NOT gate is combined with the AND gate and other gates to form more complex gates like NAND. These complex gates are composed of multiple basic gates, so they are not covered in this section.

Adder

With an understanding of how the gates work, we can now build a one-digit adder.

Let’s calculate the input and output for one-digit addition.

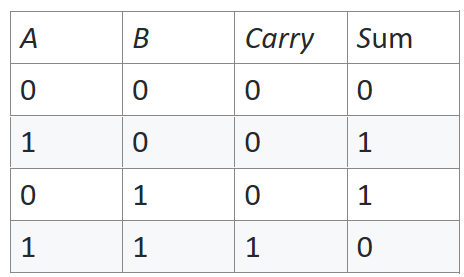
We see that the sum is the output of an XOR gate, and the carry is the output of an AND gate.

Therefore, we can construct a one-digit adder as follows.

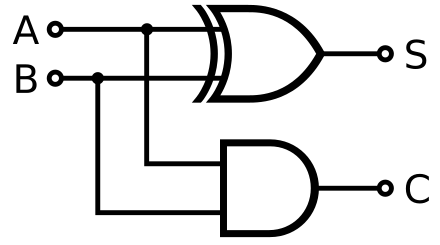
To build a full adder, we also need to consider the carry from the previous addition. This requires two one-digit adders working together.

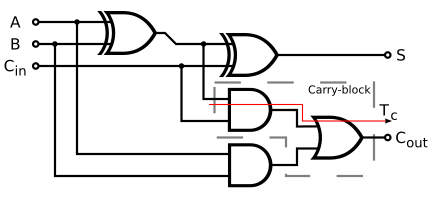
Evolution Design

Let’s revisit the evolution of the adder. We need to consider the following:

• How to implement an adder and organize points inside it.
• How to mutate the adder when it gives birth to a new adder.
• How to determine the birth rate.
• How to control the total number of gates.

During the design phase, I structured the entities into three layers:

1. Basic Layer: This consists of gates and connections. A gate calculates the output digit from two input digits, while connections determine how points are interconnected.
2. Second Layer: This layer represents the adder, which is composed of gates and connections. Using a depth-first search (DFS) algorithm, we can calculate the adder’s output given two input numbers. Note that if the connections form a loop, the adder is invalid as it cannot produce a final result.
3. Final Layer: This layer is the world, composed of multiple adders. It also stores basic information, such as birth rate, mutation rate, and the path to save results.

Birth Rate

I implemented a basic linear birth rate algorithm: base rate + k * correctness. This ensures that adders that answer addition tasks more accurately give birth to more adders.

Total Number

Similar to the real world, creatures are born and pass away, helping control the population. In our adder world, we also need to control the total number, or the computer’s memory will be overwhelmed. We can use a straightforward method: if the total number exceeds the limit, we sort the adders by their scores on addition tasks. If they have the same score, the younger adders stay.

Mutation of Adders

Mutation involves two factors: frequency and method.

Frequency: Mutations should occur infrequently with a high probability and more frequently with a lower probability. I set the first mutation rate at 0.9, the second at 0.9 * 0.9 = 0.81, the third at 0.81 * 0.81 = 0.656, and so on.

Method: This is the tricky part.

Initially, I used a mutation method focusing on adding and deleting gates, but fewer on building connections. Using a two-digit demo world, I eventually evolved an adder that answered all 16 addition tasks correctly. Here is what it looked like:

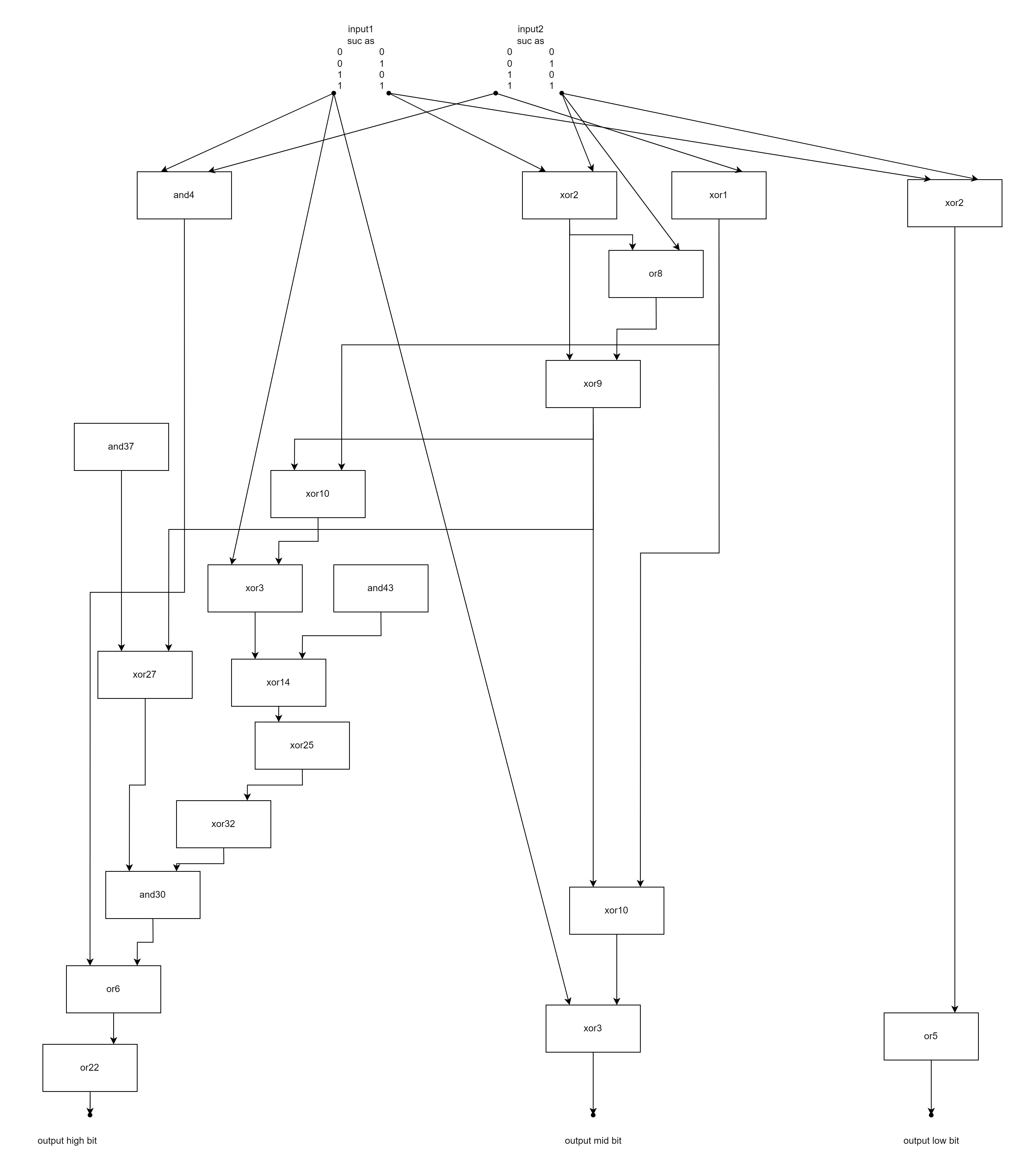
It was quite a mess. After achieving this, I modified the scoring system. Originally, it was one score for each correct addition task. I changed it so that if an adder answered all tasks correctly, it received a penalty of 0.01 * len(gates), promoting adders to reduce their gates. After running about 20,000 generations, the adder still had 9 gates, even though the optimal design had 7 gates.

So, I rethought the mutation design and made three changes:

1. When adding new gates, their connections are initialized randomly rather than connecting to nothing.
2. Allow the type of gates to change.
3. Introduce new gate types, “Left” and “Right” gates, which output from the left or right input. This makes mutations smoother.

With these modifications, I ran the world again. In just 100 generations, I obtained a beautiful adder, almost identical to our optimal design.

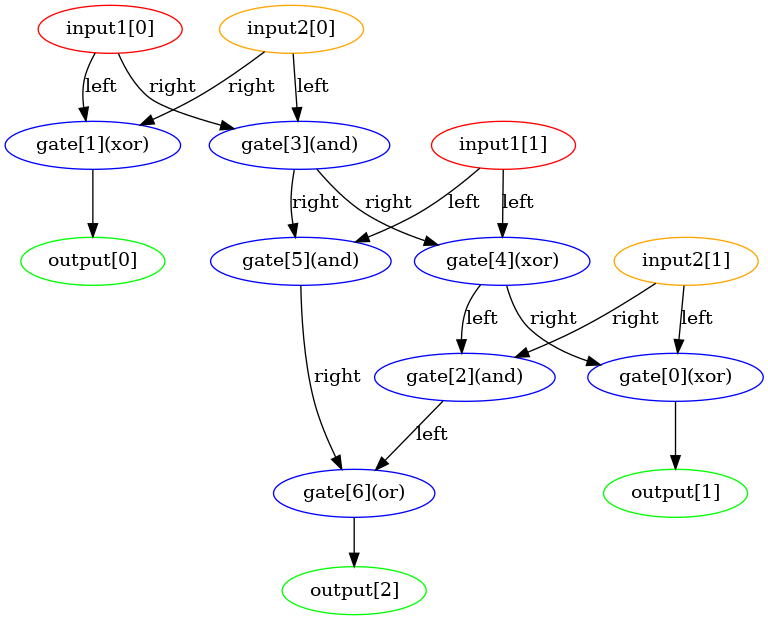
Additionally, I discovered another way to build a perfect adder, which replaced the “OR” gate with an “XOR” gate to generate the carry. Upon reflection, I realized that since the carry inputs would never both be 1, using an “OR” gate or an “XOR” gate achieved the same result.

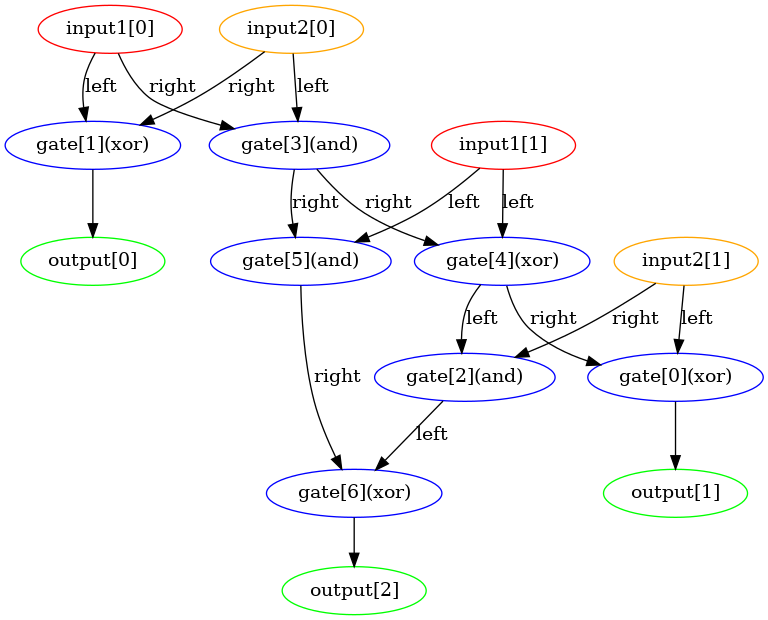
By the way, the images here are drawn using pygraphviz. Feel free to try it out in my GitHub project.

Summary

In summary, I created a world where adders mutate and give birth to new adders if they perform well in addition tasks. By making the mutation process smoother, I successfully evolved an Ace adder. It is quite impressive to see the amazing results we can achieve with randomness and reinforcement.